Blaise Pascal (1623 - 1662)
From `A Short Account of the History of Mathematics' (4th edition, 1908)
by W. W. Rouse Ball.
Among the contemporaries of Descartes none displayed greater natural
genius than Pascal, but his mathematical reputation rests more on what
he might have done than on what he actually effected, as during a
considerable part of his life he deemed it his duty to devote his whole
time to religious exercises.
Blaise Pascal was born at Clermont on June 19, 1623, and died
at Paris on Aug. 19, 1662. His father, a local judge at Clermont, and
himself of some scientific reputation, moved to Paris in 1631, partly
to prosecute his own scientific studies, partly to carry on the
education of his only son, who had already displayed exceptional
ability. Pascal was kept at home in order to ensure his not being
overworked, and with the same object it was directed that his education
should be at first confined to the study of languages, and should not
include any mathematics. This naturally excited the boy's curiosity,
and one day, being then twelve years old, he asked in what geometry
consisted. His tutor replied that it was the science of constructing
exact figures and of determining the proportions between their different
parts. Pascal, stimulated no doubt by the injunction against reading it,
gave up his play-time to this new study, and in a few weeks had discovered
for himself many properties of figures, and in particular the proposition
that the sum of the angles of a triangle is equal to two right angles.
I have read somewhere, but I cannot lay my hand on the authority, that
his proof merely consisted in turning the angular points of a triangular
piece of paper over so as to meet in the centre of the inscribed circle:
a similar demonstration can be got by turning the angular points over
so as to meet at the foot of the perpendicular drawn from the biggest
angle to the opposite side. His father, struck by this display of
ability, gave him a copy of Euclid's Elements, a book which
Pascal read with avidity and soon mastered.
At the age of fourteen he was admitted to the weekly meetings of
Roberval, Mersenne, Mydorge, and other French geometricians; from
which, ultimately, the French Academy sprung. At sixteen Pascal
wrote an essay on conic sections; and in 1641, at the age of
eighteen, he constructed the first arithmetical machine, an
instrument which, eight years later, he further improved. His
correspondence with Fermat about this time shews that he was then
turning his attention to analytical geometry and physics. He
repeated Torricelli's experiments, by which the pressure of the
atmosphere could be estimated as a weight, and he confirmed his
theory of the cause of barometrical variations by obtaining at
the same instant readings at different altitudes on the hill of
Puy-de-Dôme.
In 1650, when in the midst of these researches, Pascal suddenly
abandoned his favourite pursuits to study religion, or, as he
says in his Pensées, ``contemplate the greatness and
the misery of man''; and about the same time he persuaded the
younger of his two sisters to enter the Port Royal society.
In 1653 he had to administer his father's estate. He now took up
his old life again, and made several experiments on the pressure
exerted by gases and liquids; it was also about this period that
he invented the arithmetical triangle, and together with Fermat
created the calculus of probabilities. He was meditating marriage
when an accident again turned the current of his thoughts to a
religious life. He was driving a four-in-hand on November 23, 1654,
when the horses ran away; the two leaders dashed over the parapet
of the bridge at Neuilly, and Pascal was saved only by the traces
breaking. Always somewhat of a mystic, he considered this a special
summons to abandon the world. He wrote an account of the accident
on a small piece of parchment, which for the rest of his life he
wore next to his heart, to perpetually remind him of his covenant;
and shortly moved to Port Royal, where he continued to live until
his death in 1662. Constitutionally delicate, he had injured his
health by his incessant study; from the age of seventeen or eighteen
he suffered from insomnia and acute dyspepsia, and at the time of
his death was physically worn out.
His famous Provincial Letters directed against the Jesuits,
and his Pensées, were written towards the close of his
life, and are the first example of that finished form which is
characteristic of the best French literature. The only mathematical
work that he produced after retiring to Port Royal was the essay
on the cycloid in 1658. He was suffering from sleeplessness and
toothache when the idea occurred to him, and to his surprise his
teeth immediately ceased to ache. Regarding this as a divine
intimation to proceed with the problem, he worked incessantly
for eight days at it, and completed a tolerably full account
of the geometry of the cycloid.
I now proceed to consider his mathematical works in rather greater
detail.
His early essay on the geometry of conics, written in 1639,
but not published till 1779, seems to have been founded on the
teaching of Desargues. Two of the results are important as well
as interesting. The first of these is the theorem known now as
``Pascal's Theorem,'' namely, that if a hexagon be inscribed in
a conic, the points of intersection of the opposite sides will lie
in a straight line. The second, which is really due to Desargues,
is that if a quadrilateral be inscribed in a conic, and a straight
line be drawn cutting the sides taken in order in the points
A, B, C, and D, and the conic in P and Q, then
PA.PC : PB.PD = QA.QC : QB.QD.
Pascal employed his arithmetical triangle in 1653, but
no account of his method was printed till 1665. The triangle
is constructed as in the figure below, each horizontal line
being formed form the one above it by making every number in it
equal to the sum of those above and to the left of it in the
row immediately above it; ex. gr. the fourth number in the
fourth line, namely, 20, is equal to 1 + 3 + 6 + 10.
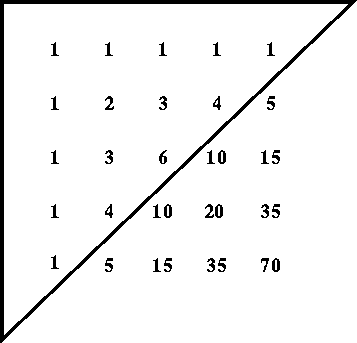
The numbers in each line are what are now called figurate
numbers. Those in the first line are called numbers of the first
order; those in the second line, natural numbers or numbers of the
second order; those in the third line, numbers of the third order,
and so on. It is easily shewn that the mth number in the nth
row is (m+n-2)! / (m-1)!(n-1)!
Pascal's arithmetical triangle, to any required order, is got by
drawing a diagonal downwards from right to left as in the figure.
The numbers in any diagonal give the coefficients of the expansion
of a binomial; for example, the figures in the fifth diagonal, namely
1, 4, 6, 4, 1, are the coefficients of the expansion
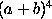Pascal used the triangle partly for this purpose,
and partly to find the numbers of combinations of m things taken
n at a time, which he stated, correctly, to be
(n+1)(n+2)(n+3) ... m / (m-n)!
Perhaps as a mathematician Pascal is best known in connection with
his correspondence with Fermat in 1654 in which he laid down the
principles of the theory of probabilities
